Potere di mercato e filiere agroalimentari

Introduzione

Nel recente passato i processi di concentrazione dell’industria alimentare e della grande distribuzione organizzata nei paesi occidentali hanno sollevato il timore di possibili comportamenti anticoncorrenziali da parte delle imprese nelle fasi intermedie delle filiere agroalimentari, a scapito dei soggetti a monte (le imprese agricole) e a valle (i consumatori finali). Tali comportamenti, definibili con il termine generale di potere di mercato, permettono alle imprese di maggiori dimensioni (comparate al mercato di appartenenza) di alzare il prezzo di vendita dei prodotti (potere oligopolistico) o di abbassare il prezzo di acquisto dei fattori (potere oligopsonistico) rispetto ai livelli che si avrebbero se i mercati fossero perfettamente concorrenziali. Per la loro importanza sia dal punto di vista pratico che teorico, il potere di mercato e la concorrenzialità lungo le filiere agroalimentari sono stati oggetto di una grande quantità di indagini, basate su differenti tipi di metodologie. Nel presente contributo verrà fornita una sintetica descrizione di tali metodologie evidenziandone vantaggi e limitazioni, indicando quindi un approccio potenzialmente unificante e presentando una sua applicazione empirica alla realtà italiana.

Metodologie di individuazione del potere di mercato

E’ possibile individuare due grandi categorie di metodi impiegati per analizzare il potere di mercato delle e nelle filiere agroalimentari: gli studi sulla trasmissione asimmetrica dei prezzi lungo la filiera e i modelli strutturali, che misurano l’esercizio del potere di mercato nei singoli mercati che compongono una filiera.

Trasmissione asimmetrica del prezzo

Secondo la teoria economica i prezzi svolgono la fondamentale funzione di segnalare agli agenti la scarsità relativa dei beni scambiati, al fine di ottimizzare l’allocazione delle risorse. Per questo motivo è importante che i segnali di prezzo vengano correttamente trasmessi tra mercati connessi orizzontalmente (stesso tipo di bene scambiato in luoghi geograficamente distanti tra loro) e verticalmente (dove il prodotto di un settore diviene fattore produttivo in quello successivo). Una trasmissione non corretta o incompleta dei prezzi lungo mercati verticalmente interrelati (filiere) può rappresentare, da un lato, un elemento di contraddizione per la teoria economica (Meyer, von Cramon-Taubadel, 2004), come dimostrato dall’ampio lavoro empirico di Peltzmann (2000), mentre dall’altro viene spesso considerata come evidenza di un comportamento anticompetitivo. In particolare, per questo secondo motivo, sono stati condotti numerosi studi su mercati verticalmente interrelati quali le filiere agroalimentari e quelle energetiche. La maggioranza di tali indagini mira ad individuare asimmetrie (all’interno di una filiera) tra le variazioni dei prezzi alla produzione della materia prima agricola e dei prezzi al consumo del prodotto alimentare. Si verifica un’asimmetria quando, per esempio, un incremento del prezzo alla produzione (agricola) è pienamente trasmesso al consumo (alimentare), mentre una riduzione del prezzo all’origine non viene trasmessa con la medesima intensità e/o istantaneità negli stadi finali della filiera. L’individuazione di tali asimmetrie è spesso imputata all’esercizio del potere di mercato in uno o più stadi della filiera; tuttavia né dal punto di vista teorico né da quello empirico si può stabilire un solido nesso di causalità tra potere di mercato e trasmissione asimmetrica del prezzo, anche in considerazione del fatto che quest’ultima può essere determinata anche da altri fattori quali costi di ri-prezzamento e di gestione dei magazzini, inflazione, informazione imperfetta e politiche con effetto sui prezzi. Se da una parte, quindi, questo tipo di modelli presenta il vantaggio di analizzare la filiera nel suo complesso ricorrendo a dati reperibili con relativa facilità (serie storiche di prezzi alla produzione e al consumo) le asimmetrie individuate non possono essere attribuite in maniera univoca all’esercizio del potere di mercato, rendendo tali analisi non utilizzabili per individuare comportamenti anticoncorrenziali.

Modelli strutturali

Tale categoria, spesso anche definita col termine Neio (New Empirical Industrial Organization), racchiude diversi modelli che hanno lo scopo di individuare la presenza o di misurare l’intensità della concorrenza imperfetta in un singolo mercato, e non dell’intera filiera (fanno eccezione i modelli multi-stadio, Moro et al., 2012) . Essi variano in base al versante del mercato indagato (offerta di prodotto, per misurare il potere oligopolistico o domanda di fattore, per misurare quello oligopsonistico), in base al tipo di prodotto scambiato (omogeneo o differenziato), in base alle caratteristiche di stima (modelli parametrici o non parametrici) e in base alla ricorsività delle scelte degli agenti (modelli statici o dinamici).
I modelli che stimano l’intensità del potere oligopolistico (statici, parametrici e a prodotto indifferenziato), si basano sull’assunto che, in concorrenza perfetta, il prezzo di vendita del prodotto eguaglia il costo marginale di produzione, azzerando gli extraprofitti delle imprese; quando il prezzo è superiore al costo marginale (costo necessario per produrre una unità aggiuntiva) si ha quindi evidenza dell’esercizio di potere di mercato dal versante dell’offerta. Sfortunatamente questo approccio non è di facile applicazione poiché le informazioni di costo delle imprese sono difficilmente reperibili e andrebbero quindi stimate. Per rilevare il potere oligopolistico si adotta spesso un'altra via, basata sulla diversa funzione di ricavo tra concorrenza e monopolio. Nella prima la quantità prodotta dalla singola impresa non influenza il prezzo di vendita, quindi il ricavo per una dose aggiuntiva di prodotto venduto (ricavo marginale) è costante e uguale al prezzo di mercato: Rmg = P. Il monopolista, al contrario, rappresentando l’intera offerta di mercato, vede il suo ricavo marginale diminuire all’aumentare della quantità venduta: Rmg = P + Q(dP/dQ) dove Q è la quantità venduta e dP/dQ è la diminuzione del prezzo conseguente all’aumento unitario di quantità venduta. Le due funzioni di ricavo marginale possono essere riassunte nella seguente espressione: Rmg = P + θQ(dP/dQ) dove θ è un parametro di condotta oligopolistica (un ragionamento simmetrico si può fare per l’oligopsonio) che varia da zero a uno. Con θ=0 si ha concorrenza perfetta mentre quando θ=1 vi è un regime di monopolio, più in generale quando θ >0 si ha esercizio di potere oligopolistico. Il valore di θ viene stimato con un sistema di equazioni strutturali che descrivono il profitto delle imprese e la domanda di mercato (Perloff et al, 2007). La descrizione proposta finora riguarda solo uno dei modelli strutturali più “semplici” da illustrare, tuttavia appare evidente quanto possa essere complesso il loro utilizzo.
Tali modelli, essendo radicati nella teoria economica, permettono non solo di individuare l’esercizio del potere di mercato, ma anche di misurarne l’intensità in modo conclusivo e univoco (esistono tuttavia critiche circa l’accuratezza del processo di stima si vedano Corts, 1999 e Perloff, 2012). Per fare ciò occorre una grande quantità di informazioni per la stima delle funzioni di domanda (o offerta) e di profitto (prezzi, quantità, reddito disponibile e altre variabili) il cui risultato rimane nella maggior parte dei casi confinato a un solo versante di uno dei mercati verticalmente interrelati che compongono una singola filiera (ad eccezione dei modelli multi-stadio).

Un approccio di sintesi

Se lo scopo è un efficace e rapido esame della concorrenzialità delle filiere agroalimentari, entrambe le categorie di metodi sinteticamente illustrati presentano pregi e limitazioni. Le analisi di trasmissione asimmetrica del prezzo sono relativamente agevoli da condurre ed esaminano l’intera filiera, ma le simmetrie o asimmetrie rilevate non rappresentano una prova conclusiva circa la presenza/assenza di potere di mercato. I modelli strutturali permettono di misurare il grado di potere di mercato, spesso in un ambito ristretto dell’intera filiera e anche quando la analizzano nella sua interezza richiedendo comunque numerose informazioni, non sempre disponibili, e l’impiego di complesse metodologie di stima. Se, come detto prima, lo scopo è di disporre di strumenti relativamente rapidi ma attendibili per individuare comportamenti anticoncorrenziali a livello di filiera, nessuna delle metodologie illustrate sembra rispondere adeguatamente ai requisiti. Sorge quindi spontanea la domanda se possa esistere un approccio che permetta di combinare il vantaggio e la rapidità di analisi a livello di filiera con il rigore e l’attendibilità dei modelli strutturali, in modo da combinare e utilizzare in modo coordinato entrambe le metodologie (Digal e Ahmadi-Esfahani, 2002). Tutti gli autori che si sono mossi su questa linea di indagine sono partiti dal lavoro di Gardner (1975) che per primo ha proposto la rappresentazione semplificata di una filiera agroalimentare in cui l’industria alimentare (che si assume essere perfettamente concorrenziale) acquista un fattore produttivo dal settore agricolo e uno dal settore non agricolo per produrre e vendere un prodotto alimentare, assumendo tecnologia a coefficienti fissi (quantità di prodotto agricolo ≈ quantità di alimento trasformato). Partendo da una situazione di equilibrio, Gardner simula gli effetti di variazioni della domanda di alimento e di offerta di fattore produttivo agricolo sul margine di mercato (differenza tra prezzo al consumo dell’alimento e prezzo del fattore produttivo agricolo). Alcuni autori hanno modificato il modello di Gardner, introducendo la possibilità che gli stadi intermedi adottino condotte non concorrenziali, costruendo così uno strumento per individuare il potere di mercato a livello di filiera. Questo è stato fatto sia da Holloway (1992) negli Stati Uniti che da McCorriston et al. (1998, 2001) e da Lloyd et al. (2006, 2009) nel Regno Unito. Il modello sviluppato da Holloway richiede, per la sua applicazione empirica, l’impiego di dati relativi a prezzi e quantità scambiate, non sempre facilmente reperibili, mentre la specificazione di Lloyd et al. utilizza dati in serie storica di prezzo alla produzione e al consumo e altre informazioni normalmente reperibili dalle fonti ufficiali di statistica economica (variabili approssimanti i costi di trasformazione e commercializzazione, le alterazioni di domanda alimentare e di offerta agricola). Questo forse è il motivo per cui questo secondo filone di indagine è stato replicato in altri studi simili condotti in vari paesi europei tra cui l’Italia (Cavicchioli, 2009 e Cavicchioli, 2010), la Polonia (Fałkowski, 2010) e la Finlandia (Niemi e Xing, 2010). In tutti i lavori sopra citati il modello di Gardner viene modificato per rendere possibile l’esercizio del potere di mercato lungo la filiera, introducendovi dei parametri (come quello illustrato nel paragrafo precedente) di condotta oligopolistica (θ) e oligopsonistica (μ); il modello deriva quindi un’equazione che descrive i fattori che influenzano il prezzo al consumo del prodotto alimentare in assenza e in presenza di potere di mercato. I primi sono il prezzo alla produzione della materia prima agricola e i costi di mercato (trasformazione e commercializzazione): in caso di esercizio del potere di mercato, agiscono anche le variabili (dette shifter) che alterano la funzione di domanda alimentare (come la variazione dei prezzi dei prodotti non alimentari) e la funzione di offerta di prodotto agricolo (come la variazione dei prezzi dei mezzi tecnici per l’agricoltura). Secondo le previsioni del modello, se tutti gli stadi della filiera sono perfettamente concorrenziali (quindi non viene esercitato né potere oligopolistico θ =0, né potere oligopsonistico μ =0) il prezzo al consumo dipende solo dal prezzo alla produzione e dai costi di mercato. Se invece viene esercitato potere di mercato in uno degli stadi della filiera (θ >0 e/o μ >0) il prezzo al consumo dipende, oltre che dal prezzo alla produzione e dai costi di mercato, anche dagli shifter di domanda alimentare e offerta agricola che agirebbero simultaneamente sul prezzo al consumo, i primi aumentandolo, i secondi riducendolo.

Un‘applicazione empirica: la filiera del latte alimentare in Italia

L’illustrazione sintetica ed esemplificata del caso empirico è tratta da Cavicchioli, 2009 e Cavicchioli, 2010, cui si rimanda per ogni dettaglio, relativo alla parte teorica, ai dati e alle procedure di stima. Le previsioni del modello teorico illustrato in precedenza richiedono l’analisi di varie informazioni in serie storica per essere testate empiricamente. Il settore analizzato (latte alimentare) è stato scelto sia perché ha tecnologia a coefficienti fissi, sia per la relativa abbondanza di dati disponibili. Per l’applicazione del modello teorico sono state impiegate informazioni in serie storica mensile che approssimassero i prezzi alla produzione e al consumo, i costi di mercato (utilizzando l’indice del costo del lavoro nel settore), e gli shifter di domanda alimentare e offerta agricola. Una descrizione sintetica delle variabili è riportata nella tabella 1.

Tabella 1 - Fonti di dati e variabili impiegate per l’analisi empirica (espresse in numeri indici)

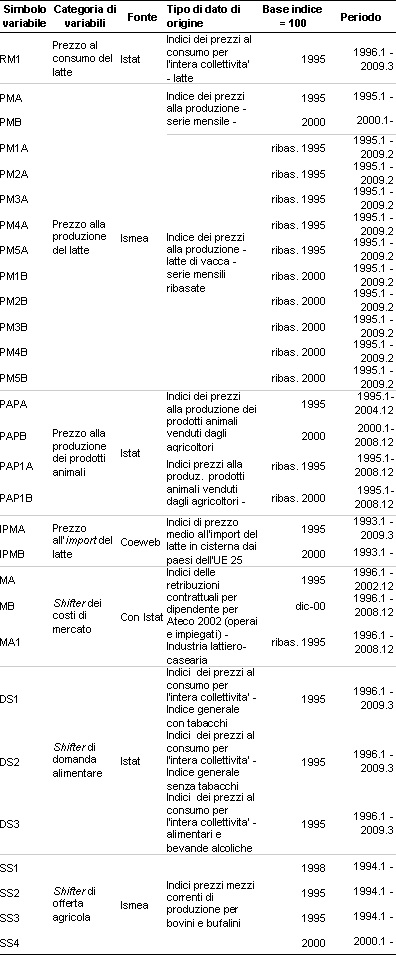
Fonte: Istat, Conistat, Coeweb, Ismea e successive elaborazioni

Sono state impiegate 29 serie storiche, rappresentate da indici di prezzo e costo, tratte da diverse fonti statistiche, di differente lunghezza e base (1995 e 2005). L’analisi è stata condotta su tre periodi: gennaio 1996 – ottobre 2003 (dati in base 1995), gennaio 2000 – ottobre 2008 (dati in base 2000) e, per sfruttare la sovrapposizione tra le due serie, gennaio 1996 –ottobre 2008. Il prezzo alla produzione è stato approssimato da diverse variabili (prezzo alla produzione e all’import del latte e dei prodotti animali), i costi di mercato dagli indici di costo del lavoro del settore (perché rappresentano una quota importante dei costi di trasformazione nei comparti manifatturieri), gli shifter di domanda alimentare da vari indici di prezzi al consumo (poiché la scelta di consumo del latte dipende dal prezzo degli altri prodotti) e gli shifter di offerta agricola dagli indici dei prezzi dei fattori produttivi per le aziende da latte (poiché ne influenzano il costo di produzione e quindi il livello produttivo).
Per testare empiricamente il modello si è fatto ricorso a un particolare tipo di analisi di regressione (modello a correzione d’errore o ECM, Engle e Granger, 1987) che individua le relazioni di lungo periodo tra variabili in serie storica quando queste presentano caratteristiche di persistenza (o non stazionarietà); le variabili medesime sono state preliminarmente sottoposte a indagini per verificare queste proprietà statistiche.
Il test empirico con l’ECM ha utilizzato come variabile dipendente il prezzo al consumo e comevariabili esplicative (cioè che influenzano la variabile dipendente) il prezzo alla produzione, i costi di mercato e gli shifter di domanda e offerta. Per ciascuno dei tre periodi esaminati sono state provate tutte le combinazioni possibili delle variabili disponibili.
I risultati dell’ECM sono plausibili dal punto di vista della teoria economica solo se sia il prezzo alla produzione che i costi di mercato hanno un effetto positivo sul prezzo al consumo. Ogni risultato differente sarebbe in contrasto con la teoria economica (e con il buonsenso). Soddisfatta questa precondizione, il test segnala concorrenza perfetta lungo la filiera se gli shifter di domanda alimentare e di offerta agricola non influenzano in modo (statisticamente) significativo il prezzo al consumo. Si verifica esercizio del potere di mercato quando, simultaneamente, lo shifter di domanda ha effetto positivo e quello di offerta ha effetto negativo sul prezzo al consumo. Ogni altro esito risulta non conclusivo circa la concorrenzialità della filiera.
Come si è visto nella tabella 1, ci sono più indici del prezzo alla produzione del latte e più indici per ogni shifer. Il test sul potere di mercato è stato condotto con tutte le possibili combinazioni di tali variabili, per aumentare la probabilità di ottenere esiti conclusivi dal test stesso. Le tabelle seguenti presentano gli effetti delle variabili esaminate sul prezzo al consumo di latte; i segni “+”, “-“ e “0” indicano che la variabile considerata ha rispettivamente effetto positivo, negativo o o sul prezzo al consumo. Per capire se una data combinazione di variabili indica o meno esercizio del potere di mercato, occorre confrontare gli effetti di tale combinazione sul prezzo al consumo, con gli effetti attesi in caso di potere di mercato o concorrenza perfetta (ultime 4 righe di ogni tabella) La tabella 2 riporta gli esiti dell’ECM del primo periodo esaminato.

Tabella 2 - Test sul potere di mercato, variabile dipendente prezzo al consumo del latte alimentare. gennaio 1996 - ottobre 2003 (91 osservazioni).

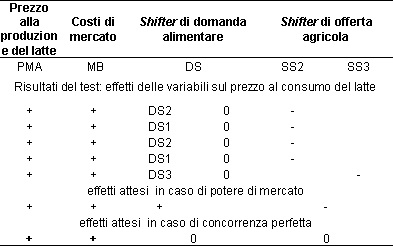
Fonte: elaborazioni su dati Istat, Conistat, Coeweb, Ismea

Come si può osservare nessuna delle combinazioni di variabili indica concorrenza perfetta o esercizio del potere di mercato, I risultati relativi a questo primo periodo non sono quindi conclusivi. Gli esiti del test nel periodo successivo sono presentati nella tabella 3.

Tabella 3 - Test sul potere di mercato, variabile dipendente prezzo al consumo del latte alimentare. gennaio 2000 - ottobre 2008 (101 osservazioni).

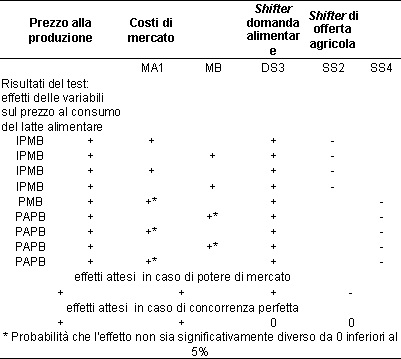
Fonte: elaborazioni su dati Istat, Conistat, Coeweb, Ismea

In questo caso 4 combinazioni di variabili delle 9 presentate indicano esercizio del potere di mercato con significatività all’1% (probabilità che l’effetto delle variabili sia o), e il medesimo risultato si ha nei restanti 5 casi con confidenza statistica inferiore circa l’effetto dei costi di mercato; Il test indica quindi esercizio del potere di mercato nel periodo esaminato. In tabella 4 è sintetizzata la parte più rappresentativa dei risultati del periodo di sovrapposizione delle serie storiche in base 1995 e 2000.

Tabella 4 - Test sul potere di mercato, variabile dipendente prezzo al consumo del latte alimentare. gennaio 1996 - ottobre 2008 (141 osservazioni).

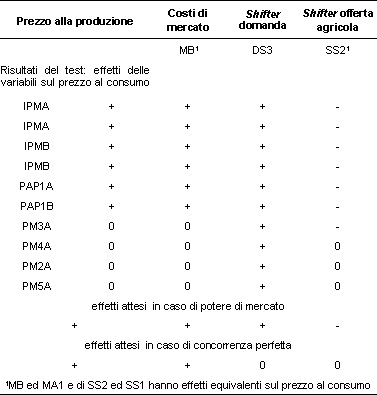
Fonte: elaborazioni su dati Istat, Conistat, Coeweb, Ismea

Per motivi di spazio vengono presentate solo 10 delle 30 combinazioni di variabili. In questo caso 6 combinazioni su 10 indicano potere di mercato lungo la filiera. Da notare come l’utilizzo del prezzo alla produzione del latte (fonte Ismea) renda non conclusive le ultime 4 combinazioni di variabili, mentre quelle che utilizzano delle proxy (prezzo alla produzione dei prodotti animali e prezzo all’import del latte) siano conclusive in favore dell’esercizio del potere di mercato (in realtà le serie di prezzo all’import non avrebbero le proprietà statistiche necessarie per poter essere usate in un Ecm, per i dettagli si vedano le pubblicazioni di riferimento).
I risultati dell’analisi indicano, dal punto di vista dei contenuti, esercizio del potere di mercato nella filiera del latte alimentare durante il periodo 2000-2008; si ricorda che tali conclusioni non sono in grado di indicare a quale livello della filiera viene esercitato il potere di mercato. Dal punto di vista metodologico è da tenere presente che, pur presentendo il vantaggio di utilizzare informazioni facilmente disponibili il test non giunge sempre a una conclusione circa la concorrenzialità lungo la filiera.

Considerazioni conclusive

La metodologia illustrata in questo contributo tenta di fornire uno strumento relativamente rapido ma attendibile per individuare la presenza di potere di mercato lungo le filiere agroalimentari, unendo i vantaggi dell’analisi di trasmissione del prezzo con la solidità dei modelli strutturali. Nell’ottica di una efficiente analisi a servizio delle autorità garanti della concorrenza, una simile metodologia potrebbe rappresentare un primo filtro di indagine speditiva per investigare se, in una o più filiere, possano verificarsi comportamenti anticoncorrenziali, nel qual caso l’indagine potrebbe essere approfondita. Questo costituirebbe un utile strumento di indagine preliminare, non quindi con lo scopo di sostituire i modelli strutturali ma bensì di cooperarvi, ponendosi rispetto ad essi nello stesso rapporto che esiste tra un medico di base e un medico specialista.
Per fare questo è tuttavia necessario una validazione di questo tipo di metodologia, poiché la sola applicazione empirica non costituisce prova del fatto che essa “funzioni”, che rilevi cioè il potere di mercato quando effettivamente presente e che indichi concorrenza perfetta quando questo è assente. La validazione può essere fatta conducendo il test del potere di mercato su dati (prezzi, costi di mercato e shifter di domanda e offerta) generati da filiere costituite artificialmente (attraverso delle simulazioni Monte Carlo) di cui è noto a priori il livello di concorrenzialità; il modello è validato se le sue conclusioni concordano con la presenza o assenza di potere di mercato stabilita a priori. In questo modo sono stati validati gli stessi modelli strutturali: sarebbe tuttavia possibile utilizzare proprio tali modelli per validare, indirettamente, il test sul potere di mercato. Si potrebbe cioè analizzare la medesima filiera con il test sul potere di mercato e con un modello strutturale multi-stadio (si veda il recente lavoro di Moro et al., 2012 sulle filiere delle carni) verificando se gli esiti del primo coincidono con le stime del secondo.
Accanto ai vantaggi, vanno sottolineate e indagate alcune carenze del test sul potere di mercato, quali la possibilità che questo non fornisca indicazioni univoche sulla concorrenzialità della filiera. Nell’applicazione empirica vista sopra questo può essere dovuto a una disomogeneità tra le fonti statistiche impiegate per i prezzi al consumo e alla produzione (Istat e Ismea), elemento che non può essere influenzato da chi conduce la ricerca. Si può invece tentare di migliorare le variabili che approssimano i costi di mercato e gli shifter, creando degli indici composti che catturino il vero effetto di tali variabili sul prezzo al consumo. Infine andrebbe fatto un ulteriore sforzo sul versante teorico per riformulare il modello permettendo la variabilità dei coefficienti input/output. Molte sono quindi le direzioni in cui muoversi per migliorare strumenti e modalità di indagine della concorrenzialità delle filiere; chi scrive è desideroso di collaborare con quanti condividono questo interesse di ricerca, che ha anche importanti ricadute operative.

Riferimenti bibliografici

• Cavicchioli D (2009) L'analisi di trasmissione del prezzo lungo la filiera agro-alimentare per individuare l'esercizio del potere di mercato. Tesi di Dottorato, Padova [pdf]

• Cavicchioli D (2010), Detecting market power along food supply chains: evidence from the fluid milk sector in Italy, Paper presented at the 116th Eaae seminar, Parma, 27-30 October, 2010 [pdf]

• Corts K.S. (1999), Conduct parameters and the measurement of market power, Journal of Econometrics, vol. 88: 2

• Digal, L. N., Ahmadi-Esfahani F. Z (2002), Market Power Analysis in the Food Industry: a Survey of Methods. Australian Journal of Agricultural and Resource Economics, vol. 46:4.

• Engle R.F., Granger C. W. J (1987), Co-integration and error correction: representation, estimation and testing, Econometrica, n. 2

• Fałkowski J (2010), Price transmission and market power in a transition context: evidence from the Polish fluid milk sector, Post-Communist Economies, n. 4

• Gardner, B.L (1975), The Farm-Retail Price Spread in a Competitive Food Industry, American Journal of Agricultural Economics, Issue 3

• Holloway, G. J (1991), The Farm-Retail Price Spread in an Imperfectly Competitive Food Industry, American Journal of Agricultural Economics, Issue 4

• Lloyd T., McCorriston S., Morgan W., Rayner T (2006), Food Scares, Market Power and Price Transmission: the UK Bse Crisis, European Review of Agricultural Economics, Issue 2.

• Lloyd T., McCorriston S. , Morgan W., Rayner T., Weldegebriel H (2009), Buyer Power in UK Food Retailing: A ‘First-Pass’ Test, Journal of Agricultural and Food Industrial Organization, Vol 7

• Meyer J., von Cramon-Taubadel S (2004), Asymmetric price transmission: a survey, Journal of Agricultural Economics, Issue 3

• McCorriston, S., Morgan, C.W. e Rayner, A.J. (1998), Processing Technology, Market Power and Price Transmission, Journal of Agricultural Economics, Issue 2

• McCorriston S., Morgan C.W.,  Rayner A.J. (2001), Price transmission: the interaction between market power and returns to scale, European Review of Agricultural Economics, Issue 

• Moro D., Sckokai P., Veneziani M (2012), Multi-stage Market Power in the Italian Fresh Meat Industry, Paper prepared for the Aaea meeting, Seattle, Washington, August 12-14, 2012 [pdf]

• Niemi J., Xing L (2010), First filter test of market power in Finnish food retailing sector, , Paper presented at the 116th Eaae seminar, Parma, 27-30 October, 2010 [pdf]

• Peltzman S (2000), Prices rise faster than they fall, Journal of Political Economy, n.3.

• Perloff J.M., L.S. Karp e Golan A. (2007), Estimating Market Power and Strategies, Cambridge University Press, New York

• Perloff J.M.(2012),Collinearity in Linear Structural Models of Market Power, Review of Industrial Organization, n. 2