Introduzione1
L’instabilità dei prezzi registratasi negli ultimi anni nel contesto dei mercati agro-alimentari mondiali ed europei ha portato ad un aumentato interesse dei media e della politica per questo problema, evidenziando l'andamento insoddisfacente dei margini di commercializzazione e della trasmissione delle variazioni dei prezzi (d'ora in avanti semplicemente “trasmissione dei prezzi”) lungo la catena alimentare. Secondo una recente comunicazione della Commissione (COM 2009 (591)) “un migliore funzionamento della filiera alimentare è di fondamentale importanza oltre che per i consumatori anche per assicurare una redistribuzione più sostenibile del valore aggiunto lungo la filiera, contribuendo così ad innalzare la competitività globale”.
D'altra parte il grado di trasmissione dei prezzi dalle materie prime agricole ai prodotti per il consumo ha anche un impatto non trascurabile sui trend inflattivi (o deflattivi), considerato che i prodotti alimentari incidono per il 20% sui consumi dell'Eurozona (Ferrucci et al. 2010; National Bank of Belgium, 2008). A questo si aggiunge il possibile impatto della riforma della PAC che è stato oggetto di studi finanziati dal Parlamento europeo (CEAS, 2007) e dal DEFRA (London Economics, 2004).
Anche alcune istituzioni italiane hanno commissionato studi su questi aspetti. Il Ministero dello Sviluppo Economico ha recentemente pubblicato uno studio sulla dinamica dei prezzi lungo la filiera del grano (IPI, 2008). L’Autorità Italiana Antitrust (AGCM, 2007; Giangiulio e Mazzantini, 2010), interessata alla presenza di potere di mercato in alcuni stadi della filiera agroalimentare, ha condotto un'indagine conoscitiva sulla distribuzione agroalimentare per indagare eventuali pratiche anti-concorrenziali lungo la catena di commercializzazione.
Sorprendentemente, nonostante la trasmissione dei prezzi e l'andamento dei margini abbiano attratto così tanto interesse a livello dei policy makers, pochi studi scientifici affrontano questo argomento in Italia. Frey e Manera (2007) in una recente rassegna della letteratura elencano solo 4 lavori sui mercati italiani su un totale di 64 e tutti sulle benzine.
La gran parte della letteratura sulla trasmissione dei prezzi concerne lo studio delle elasticità di trasmissione, ovvero della percentuale di variazione del prezzo in una fase della filiera che si trasmette alla fase successiva o alla fase precedente a seconda della direzione della trasmissione. Alcuni studi indagano anche l'eventuale asimmetria nella trasmissione, il fenomeno per cui incrementi e decrementi di prezzo si trasmettono in modo differente. Questo campo di studi, di carattere essenzialmente econometrico, ha vissuto durante gli anni Ottanta la cosiddetta “rivoluzione della non stazionarietà” con l’applicazione del concetto di cointegrazione (Meyer and Von Cramon Taubadel, 2004).
Una serie è detta “non stazionaria” quando si muove nel tempo senza seguire un trend deterministico (crescente o decrescente), bensì in maniera erratica. Il più noto esempio di serie non stazionaria è la cosiddetta passeggiata casuale (random walk): una serie la cui realizzazione, in ciascun periodo, è data dal valore della serie nel periodo precedente a cui si aggiunge un shock casuale. Il grafico di un random walk cresce o diminuisce nel tempo senza un disegno preciso. Due o più serie non stazionarie tuttavia possono essere “cointegrate” quando la loro relazione nel lungo periodo è stabile e può essere catturata da un'equazione i cui residui sono stazionari.
Solo recentemente è emersa la possibile confusione tra la non stazionarietà di una serie storica e la presenza di cambiamenti (break) strutturali (Boetel e Liu, 2008). Tuttavia, solo pochi studi sui prezzi alimentari si sono mossi all'interno di questo nuovo quadro di riferimento. Se si tiene conto dei possibili cambiamenti strutturali, è possibile verificare come molte serie apparentemente non stazionarie siano in realtà stazionarie (Wang e Tomek, 2007). Inoltre, Boetel e Liu (2008) trovano relazioni di cointegrazione per la filiera suinicola e bovina degli USA solo dopo aver considerato possibili cambiamenti strutturali. Adachi e Liu (2009) identificano diversi regimi che si succedono nel tempo per la relazione tra prezzi alla produzione e al consumo di maiale in Giappone.
La recente instabilità dei prezzi richiede un'analisi dei cambiamenti avente carattere strutturale nelle relazioni tra i prezzi della filiera agroalimentare. E' infatti plausibile che la recente bolla dei prezzi abbia influenzato anche i processi di formazione dei margini nelle filiere sia per le possibilità speculative offerte dall'aumentata variabilità, sia per l'attuazione di comportamenti tesi a fronteggiare il rischio. Scopo di questa nota è di fornire una prima analisi della trasmissione dei prezzi in tre filiere agroalimentari italiane all'interno di un quadro di analisi che tenga conto di possibili variazioni strutturali nelle relazioni tra prezzi.
Le metodologie illustrate sono state applicate a tre filiere alimentari italiane per le quali sono disponibili le serie di prezzi alla produzione, all'ingrosso (o del prodotto trasformato industrialmente) e al consumo: pasta, agnello e maiale. In primo luogo è stata verificata la stazionarietà della serie dei prezzi, successivamente sono stati condotti test per l’eventuale presenza di cointegrazione tra le coppie di serie. Infine sono state stimate le date dei cambiamenti strutturali nelle relazioni tra serie con la procedura di Bai e Perron (1998), individuando regimi all'interno dei quali è possibile analizzare relazioni stabili di lungo periodo.
Dati
I dati sui prezzi alla produzione, all'ingrosso e al dettaglio per pasta, agnello e maiale provengono dalla banca dati Datima e dal panel delle famiglie Ismea-Nielsen e sono stati forniti da Ismea2. Il set originale di dati contiene serie storiche a frequenza mensile dei prezzi alla produzione e all'ingrosso da gennaio 1994 a dicembre 2008 e serie dei prezzi al consumo da febbraio 2000 a giugno 20103. Datima è una raccolta di basi di dati statistici sui mercati agricoli, mentre Ismea-Nielsen è un panel per l'analisi dei consumi alimentari domestici. I dati sui prezzi fanno riferimento a categorie aggregate di prodotti.
I prezzi agricoli mensili di agnello e maiale sono in euro per Kg di peso vivo. I prezzi all'ingrosso e al dettaglio dei tagli di agnello e di maiale, del grano duro, della semola e della pasta sono in Euro per kg. L'analisi è stata effettuata sul periodo dal febbraio 2000 al giugno 2010, per il quale sono disponibili dati per tutte le fasi della filiera. Tutte le serie sono state trasformate in logaritmi naturali e destagionalizzate regredendo la serie trasformata su variabili dicotomiche mensili.
Stazionarietà delle singole serie
La presenza di relazioni stabili di trasmissione dei prezzi tra coppie di serie richiede che entrambe le serie storiche siano stazionarie o, in alternativa, che entrambe siano non stazionarie (ovvero integrate di ordine 1) ma tra loro cointegrate. E' quindi necessario esaminare in primo luogo le proprietà statistiche delle singole serie.
Le stazionarietà delle serie sono state controllate sia con un test convenzionale Augmented Dickey Fuller (1979), o ADF, sia con il test di Zivot e Andrews (1992), o ZA, che tiene conto della presenza di un break strutturale nella serie. Entrambi i test possono essere condotti in diverse specificazioni. Quelli per cui si riportano i risultati in tabella 1 considerano la presenza di una costante nel processo di generazione della serie storica per la filiera della pasta e del maiale, per quella dell'agnello è stato inserito anche un trend.
Il test ADF confronta semplicemente il comportamento di serie che non cambiano mai il loro trend (stazionarie) con quello di serie che lo cambiano in continuazione (non stazionarie). Il test suggerisce l'assenza di stazionarietà per tutte le serie dato che l'ipotesi a di non stazionarietà non può mai essere rifiutata al livello del 5% di significatività (Tabella 1).
Al contrario, il test ZA fornisce un quadro diverso. Se si consente uno shift della serie oppure un break nel trend temporale (ovvero una rottura di pendenza nella linea di trend), l'ipotesi a di un processo non stazionario viene respinta in tre delle nove serie. In questi casi, l'introduzione di un cambiamento strutturale permette di identificare nei due regimi livelli o trend diversi per i prezzi dei prodotti.
Tabella 1 - Test di non stazionarietà per le serie dei prezzi
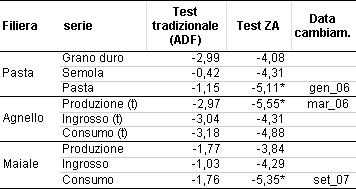
Fonte: ns. elaborazioni su dati ISMEA. * test significativo al livello 5%: si rifiuta l'ipotesi a di assenza di cointegrazione per i test EG e GH, si rifiuta l'ipotesi a di cointegrazione per il test CS
Cointegrazione tra coppie di serie
Anche se alcune delle serie esaminate attraverso i test di radice unitaria sono risultate essere stazionarie con una rottura del trend, abbiamo eseguito comunque i test di cointegrazione per tutte le coppie possibili di serie per le tre fasi di commercializzazione: produzione-consumo, ingrosso (o industria)-consumo e produzione-ingrosso (o industria). Sono stati effettuati il test convenzionale di Engle e Granger (EG) (1987) e due test che considerano un break nella relazione di cointegrazione: Gregory e Hansen (GH) (1996) e Carrion y Silvestre e Sanso (CS) (2006). Si noti che il test CS , a differenza degli altri due, ha come ipotesi a la presenza di cointegrazione. Al fine di mantenere la comparabilità tra le prove abbiamo sempre incluso nella equazione di lungo periodo tra le serie una costante. Nel caso dei test con break strutturale il cambiamento interessa sia la costante sia il coefficiente del prezzo.
I risultati dei test sono riportati in tabella 2. Una relazione di cointegrazione è confermata in EG e GH ma non in CS, per la coppia di serie alla produzione e al dettaglio della carne di agnello. È interessante notare che non possiamo rifiutare l'ipotesi a di assenza di cointegrazione secondo EG nei casi del grano duro-semola, dell'agnello ingrosso-consumo e del maiale produzione–ingrosso, mentre questa coppie di serie sembrano essere cointegrate una volta introdotto un break. Si è deciso quindi di adottare un approccio conservativo e procedere con l'analisi dei break strutturali solo per quelle coppie di serie che passano entrambi i test di cointegrazione GH e CS.
Tabella 2 - Test di cointegrazione per le serie dei prezzi
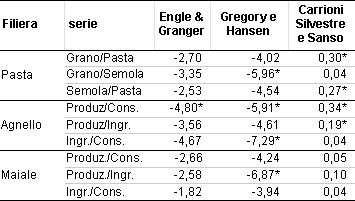
Fonte: ns. elaborazioni su dati ISMEA. * test significativo al livello 5%: si rifiuta l'ipotesi a di assenza di cointegrazione per i test EG e GH, si rifiuta l'ipotesi a di cointegrazione per il test CS
Cambiamento strutturale e regimi di trasmissione del prezzo
Per stimare le date di break per le tre relazioni di cointegrazione illustrate sopra, abbiamo utilizzato l’algoritmo di programmazione dinamico di Bai e Perron (1998, 2003) come implementato da Zeileis et al (2005). L'algoritmo fornisce intervalli di confidenza per le date di break che sono valide solo per le relazioni tra variabili stazionarie. Tuttavia le stime puntuali rimangono coerenti anche per variabili non stazionarie ma cointegrate (Kejriwal e Perron, 2008).
Tabella 3 - Regimi e date del cambiamento strutturale
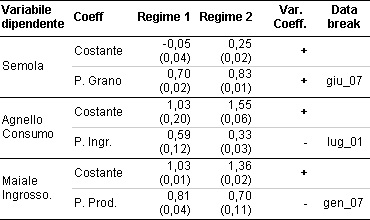
Fonte: ns. elaborazioni su dati ISMEA. Serie dei prezzi in logaritmi. Errori standard fra parentesi
Per ogni possibile coppia, abbiamo calcolato un test per un singolo break in data incognita contro un’ipotesi a di assenza di cambiamento strutturale. Sono stati anche effettuati test per stimare il numero di breakpoints. Si tratta di test che confrontano la bontà di adattamento ai dati dell'equazione quando si aggiungono variabili dicotomiche ed interazioni per un numero crescente di breakpoints. Anche se i risultati avrebbero suggerito per alcune serie (in particolare agnello e pasta) un maggior numero di breaks, abbiamo mantenuto un break unico dato il numero relativamente limitato di osservazioni. La tabella 3 mostra le stime delle date dei cambiamenti strutturali e dei coefficienti per ogni regime. Tutte le equazioni comprendono una costante. Il coefficiente del prezzo della fase a monte della filiera rappresenta una stima dell'elasticità di trasmissione perché le serie sono espresse in logaritmi.
Figura 1 - Prezzi nominali in logaritmi naturali - grano duro - semola di grano duro
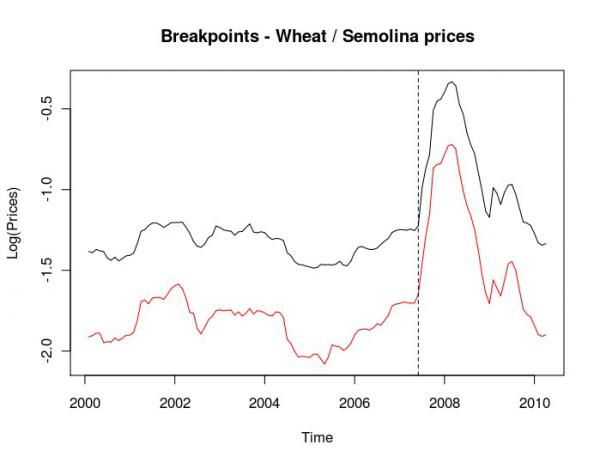
Note: Prezzi semola (in nero) / Prezzi grano duro (in rosso)
Figura 2 - Prezzi nominali espressi in logaritmi naturali - ingrosso-consumo, agnello
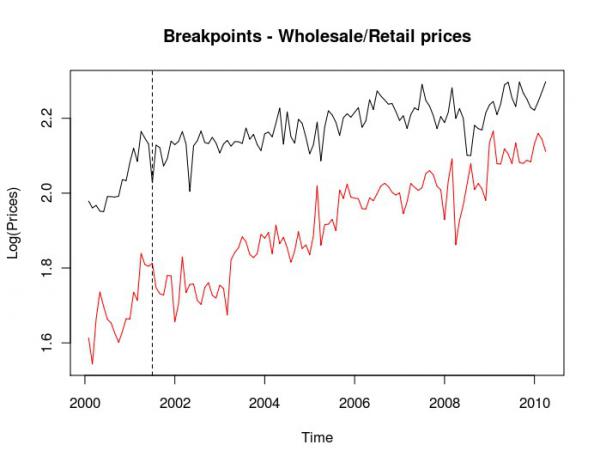
Note: Prezzi al consumo (in nero) / Prezzi all'ingrosso (in rosso)
Figura 3 - Prezzi nominali espressi in logaritmi naturali - produzione-ingrosso, maiale

Note: Prezzi all'ingrosso (in nero) / Prezzi alla produzione (in rosso)
Per quanto concerne la filiera della pasta (Figura 1), la data del break sembra essere connessa con l'inizio della bolla delle commodities. Le stime dei coefficienti di equilibrio suggeriscono che l’elasticità di trasmissione aumenta nel periodo della bolla delle commodities. Il risultato è una maggiore reattività dei prezzi della semola alle variazioni dei prezzi del grano duro. L'effetto complessivo sui margini (intesi come rapporto tra prezzo a valle e prezzo a monte) dipende dall'andamento del prezzo del grano che, dopo il break, inizialmente sale e poi scende. Inftti i margini sono dati da dalla differenza tra il logaritmo del prezzo a valle (Pdw) e il logaritmo del prezzo a monte (Pup) e quindi risulta:
Margine = Pdw-Pup = a +(b-1)*Pup
dove a e b sono rispettivamente la costante ed il coefficiente del prezzo nell'equazione di trasmissione dei prezzi della tabella 3. Con prezzi del grano stabili si sarebbe probabilmente osservato un aumento dei margini.
Per la coppia agnello all'ingrosso e al dettaglio (Figura 2) l'elasticità di trasmissione decresce dopo il break. Tuttavia, l’intercetta aumenta. Nel secondo regime, i margini tendono a diminuire poiché la crescita dei prezzi all'ingrosso è solo in parte trasmessa alla fase di vendita al dettaglio.
Infine, per l’equazione della trasmissione del prezzo per il maiale (Figura 3) il cambiamento si verifica di nuovo all'inizio della bolla delle commodities. Il regime durante la bolla è caratterizzato da una intercetta maggiore ma con una minore elasticità della trasmissione, come nel caso dell'agnello. Poiché il prezzo alla produzione non mostra alcun trend definito questo si traduce in margini più ampi per il prevalere dell'effetto intercetta sulla diminuzione dell'elasticità.
Nel corso del periodo considerato, la filiera della carne di maiale italiana è stata interessata da processi di concentrazione del settore della macellazione. Nel contesto della crisi dei prezzi 2007-09, questo fatto potrebbe avere avuto un' influenza anche sul meccanismo di trasmissione dei prezzi. Per l'agnello invece il break si pone a ridosso della seconda crisi della BSE . L'accentuata dinamica dei prezzi all'ingrosso a partire dal 2001 riflette peraltro l'analogo aumento dei prezzi all'importazione delle carni ovine. In questo caso l'alterazione del meccanismo di trasmissione potrebbe essere stata causata da variazioni strutturali all'interno della filiera legate alle crisi della BSE.
Conclusioni
In questa nota è stata condotta un’analisi delle elasticità di trasmissione dei prezzi nel lungo periodo in tre diverse catene alimentari italiane (pasta, agnello e maiale) considerando anche la presenza di break strutturali. Nell’ambito dell’analisi di cointegrazione con break strutturale è stata rilevata una relazione di equilibrio per le coppie di prezzi grano duro-semola, ingrosso-dettaglio della carne di agnello e produzione-ingrosso del maiale.
Nel caso della pasta il break strutturale si colloca all'inizio della bolla dei prezzi del 2007-09. Sia la variazione dell'intercetta sia quella dell'elasticità sono positive suggerendo un potenziale aumento dei margini che tuttavia sono influenzati anche dall'andamento variabile del prezzo del grano duro. Anche la filiera suina mostra un break strutturale all'inizio della bolla del 2007-09. In questo caso il forte aumento dell'intercetta nell'equazione di trasmissione dei prezzi è alla base dell'aumento dei margini osservabile. Questi risultati sembrano suggerire un impatto significativo della bolla e dell'aumentata volatilità dei prezzi anche sui meccanismi di trasmissione del prezzo lungo le filiere agroalimentari. Un caso a parte è invece quello dell'agnello dove il break si manifesta dopo la crisi della BSE del 2001. Qui la riduzione dell'elasticità di trasmissione, unitamente alla crescita dei prezzi all'ingrosso della carne di agnello, ha provocato una continua riduzione dei margini tra questa fase della filiera e la distribuzione al dettaglio.
L'analisi qui condotta dell'elasticità di trasmissione del prezzo potrebbe essere estesa allo studio di possibili asimmetrie nel meccanismo di trasmissione. Ulteriori ricerche sono comunque necessarie per lo studio dei prezzi alimentari con una gamma più ampia di test basandosi anche sulla recente letteratura sul cambiamento strutturale applicata alle serie storiche finanziarie e macroeconomiche.
Riferimenti bibliografici
-
Adachi K., Liu D.J. (2009), “Estimating Long-Run price relationship with structural change of unknown timing: an application to the Japanese pork market”, American Journal of Agricultural Economics, 91, pp. 1440-1447
-
AGCM (2007), Indagine conoscitiva sulla distribuzione agroalimentare, Indagini Conoscitive, 28, Autorità garante per la Concorrenza e il Mercato, Roma
-
Agra CEAS (2007),The Gap between Producer Prices and the Price paid by the Consumer, European Parliament, Brussels
-
Bai J., Perron P. (1998), “Estimating and Testing Linear Models with Multiple Structural Changes”, Econometrica, 66, pp. 47-78
-
Bai J., Perron P. (2003), “Computation and Analysis of Multiple Structural Change Models”, Journal of Applied Econometrics, 18, pp. 1-22
-
Boetel B. L., Liu D. J. (2008), Incorporating Structural Changes in Agricultural and Food Price Analysis: An Application to the U.S. Beef and Pork Sectors, Working Papers 44076, University of Minnesota, The Food Industry Center, Minneapolis
-
Carrion-i-Sylvestre J.L., Sansó-i-Rosselló A.S. (2006), “Testing the hypothesis of cointegration with structural breaks”, Oxford Bulletin of Economics and Statistics, 68, pp. 623-646
-
Commission of the European Communities (2009) - A better functioning food supply chain in Europe - Brussels 28.10.09 - COM 2009(591). Available at [link]
-
Dickey D.A., Fuller W.A. (1979), “Distribution of the estimators for autoregressive time series with a unit Root”, Journal of the American Statistical Association, 74, pp. 427-431
-
Engle R. F., Granger C.W.J. (1987), “Co-integration and error correction: representation, estimation and testing”, Econometrica, 55, pp. 251-276. Frey G., Manera M. (2007), “Econometric Models Of Asymmetric Price Transmission", Journal of Economic Surveys, 21(2), pp. 349-415
-
Mazzantini G. (2010). “Il trasferimento dei prezzi lungo le filiere agroalimentari: una possibile metodologia di analisi per i profili di interesse Antitrust”, XLVII Convegno SIDEA, Campobasso
-
Gregory A.W., Hansen B.E. (1996), “Tests for cointegration in models with regime and trend Shifts”, Oxford Bulletin of Economics and Statistics, 58, pp. 555-60
-
IPI (2008), Le dinamiche dei prezzi nella filiera del frumento, Istituto per la Promozione Industriale, Roma
-
Kejriwal M., Perron P. (2008), “The limit distribution of the estimates in cointegrated regression models with multiple structural changes”, Journal of Econometrics, 146, pp. 59-73
-
London Economics (2003), Investigation of the determinants of farm-retail price spreads. Report prepared for the Department for Environment, Food and Rural Affairs. DEFRA, London. Available at [link]
-
Meyer, J., von Cramon-Taubadel S. (2004), “Asymmetric Price Transmission: A Survey”, Journal of Agricultural Economics, 55, pp. 581-611
-
Wang, D., Tomek W.G. (2007), “Commodity Prices and Unit Root Tests”, American Journal of Agricultural Economics, 89, pp. 873-889
-
Zeileis A., Leisch F., Kleiber C., Hornik K. (2005), Monitoring Structural Change in Dynamic Econometric Models, Journal of Applied Econometrics, 20(1), pp. 99-121
-
Zivot E., Andrews D.W.K. (1992), Further evidence on the great crash, the oil price shock and the unit root hypothesis, Journal of Business and Economic Statistics, 10, pp. 251-270
- 1. La ricerca è stata effettuata grazie ad un finanziamento della Regione Toscana-Direzione Generale Organizzazione e Sistema Informativo
- 2. I dati sono stati forniti nell'ambito di un protocollo d'Intesa tra ISMEA e DIPSA-Università di Firenze
- 3. I dati, forniti da ISMEA come medie quadrisettimanali sono stati successivamente attribuiti ai 12 mesi dell'anno con un sistema di pesi proporzionali al numero di giorni delle quattro settimane ricadenti in ciascun mese


Comments
Utente non regi... (not verified)
Thu, 01/01/1970 - 01:00
Permalink
definizione di stazionarietà
Caro Gianluca, nel testo riporti questa definizione: ''Una serie è detta non stazionaria quando si muove nel tempo senza seguire un trend deterministico (crescente o decrescente), bensì in maniera erratica...'', a me sembra che questa sia la definizione di Stazionarietà.
Riporto la definizione:
La definizione di stazionarietà si divide in due forme, debole e forte, di cui la seconda talmente restrittiva e poco riscontrabile, che non verrà menzionata. Nell'accezione che qui interessa, (la forma debole) definiamo stazionario quel processo stocastico che rispetti le seguenti condizioni:
La definizione di stazionarietà si divide in due forme, debole e forte, di cui la seconda talmente restrittiva e poco riscontrabile, che non verrà menzionata. Nell'accezione che qui interessa, (la forma debole) definiamo stazionario quel processo stocastico che rispetti le seguenti condizioni:
1 - livello medio della serie;
2 - varianza inferiore a infinito
3 - covarianza fra Xt e Xt-k = G (k)
Con µ, σ2 e γ(k) indipendenti dal tempo; σ2 con un valore finito; γ(k) dipendente solo da K. Un esempio di processo stazionario è il White Noise (WN), nel quale le variabili casuali hanno una distribuzione indipendente ed egualmente distribuita.
La definizione di stazionarietà si divide in due forme, debole e forte, di cui la seconda talmente restrittiva e poco riscontrabile, che non verrà menzionata. Nell'accezione che qui interessa, (la forma debole) definiamo stazionario quel processo stocastico che rispetti le seguenti condizioni:
Con µ, σ2 e γ(k) indipendenti dal tempo; σ2 con un valore finito; γ(k) dipendente solo da K. Un esempio di processo stazionario è il White Noise (WN), nel quale le variabili casuali hanno una distribuzione indipendente ed egualmente distribuita.
Con µ, σ2 e γ(k) indipendenti dal tempo; σ2 con un valore finito; γ(k) dipendente solo da K. Un esempio di processo stazionario è il White Noise (WN), nel quale le variabili casuali hanno una distribuzione indipendente ed egualmente distribuita.
Commento originariamente inviato da 'rosa franco' in data 12/06/2011.
Utente non regi... (not verified)
Thu, 01/01/1970 - 01:00
Permalink
definizione di stazionarietà
Erratico significa ''vagabondo'' e mi sembra che renda bene l'idea di una serie che si muove senza un pattern ben definito nel tempo. Per movimento ''erratico'' comunque si deve intendere un movimento casuale nella direzione e nell'ampiezza (quindi non oscillante intorno ad una media né con varianza e covarianza stabili nel tempo). Non è una definizione precisa ma cosa si intende per passeggiata casuale (o aleatoria) è riportato subito dopo nel testo.
Commento originariamente inviato da 'Gianluca Stefani' in data 12/06/2011.